In the field of mechanical and structural engineering, understanding the stress distribution in thin-walled pressure vessels is fundamental to ensuring the safe and efficient design of numerous engineering components. Among the various geometries of pressure vessels, cylindrical shells are among the most commonly encountered due to their practical advantages in manufacturing, space utilization, and connection possibilities.
When cylindrical pressure vessels are subjected to internal pressure, they experience two distinct types of stress: longitudinal (or axial) stress and hoop (or circumferential) stress. While hoop stress typically governs the design due to its higher magnitude, longitudinal stress is equally important for ensuring structural integrity and must be properly understood and calculated.
Introduction to Longitudinal Stress
Longitudinal stress, also known as axial stress, is the stress that acts parallel to the axis of a cylindrical pressure vessel. This stress develops as a result of the internal pressure acting on the end caps or closures of the cylinder, creating forces that tend to elongate or compress the cylindrical shell along its length.
Unlike hoop stress, which acts tangentially around the circumference of the cylinder, longitudinal stress acts along the length of the cylinder. This directional difference results in different stress magnitudes and failure modes, making it essential to analyze both stress components in pressure vessel design.
The analysis of longitudinal stress is particularly important in applications where the cylinder is restrained from expanding axially, where thermal effects are significant, or where external loads are applied along the cylinder axis in addition to internal pressure.
Definition and Characteristics
Longitudinal stress is defined as the stress component that acts parallel to the longitudinal axis of a cylindrical pressure vessel. It is one of the two primary stress components that develop in thin-walled cylindrical shells under internal pressure, the other being hoop stress.
Key characteristics of longitudinal stress include:
- Direction: Acts parallel to the cylinder axis
- Uniformity: Assumed uniform through the wall thickness in thin shells
- Magnitude: Typically half the magnitude of hoop stress in simple cases
- Sign: Tensile for internal pressure (cylindrical expansion tendency)
- Distribution: Uniform around the circumference at any cross-section
In most engineering applications involving internal pressure, longitudinal stress is tensile, meaning it tends to elongate the cylinder along its axis. However, external pressure or other loading conditions can result in compressive longitudinal stress.
Force Analysis
To understand longitudinal stress, we need to analyze the forces acting on a cylindrical pressure vessel when it is subjected to internal pressure. This analysis is based on the principle of equilibrium and involves considering the forces acting on a transverse cross-section of the cylinder.
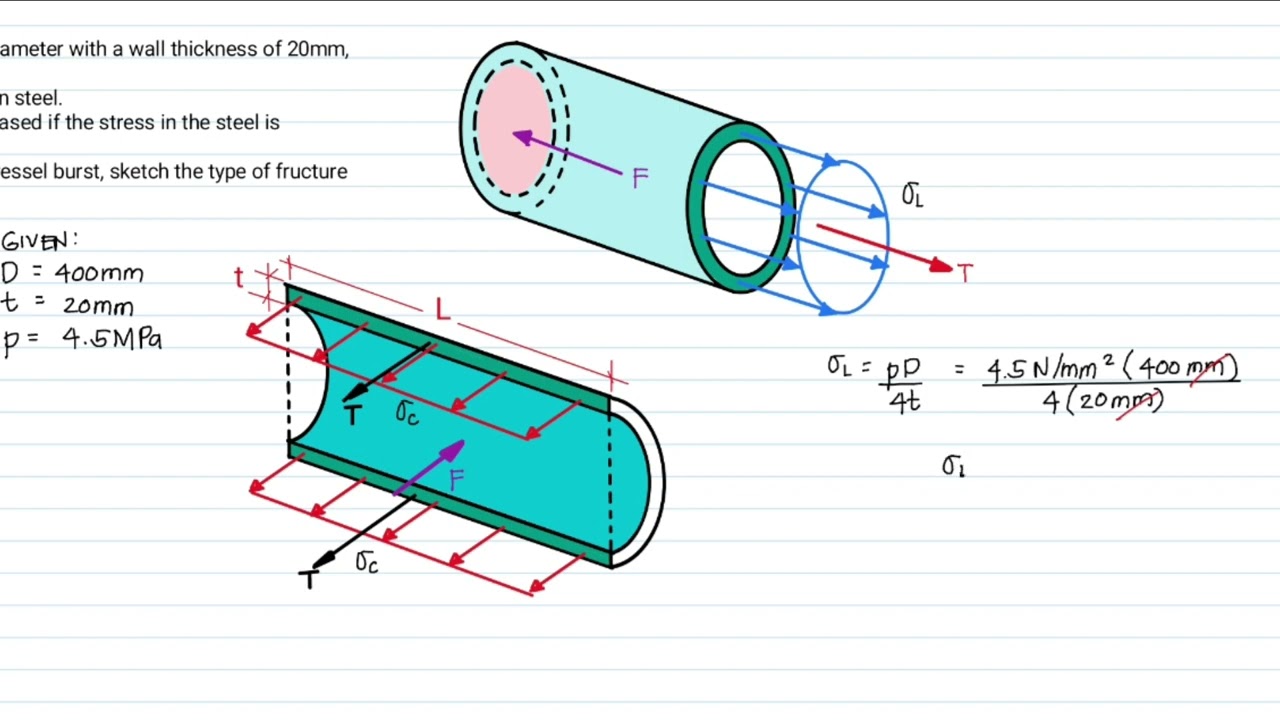
Bursting Force Acting on End Cap
When a cylindrical vessel is subjected to internal pressure, the pressure acts uniformly on the internal surfaces, including the end caps. To analyze the longitudinal stress, consider making a transverse cut through the cylinder at any point along its length.
The internal pressure p acts on the projected circular area of the end cap. The bursting force can be calculated as:
Where:
- F_burst is the total bursting force acting on the end cap
- p is the internal pressure
- r is the internal radius of the cylindrical shell
This force acts perpendicular to the end cap surface and tends to push the end cap away from the cylindrical section.
Resisting Force in the Material Wall
The material of the cylindrical shell wall resists the bursting force through longitudinal stress. To calculate the resisting force, we need to consider the stress distribution in the wall at the cut section.
In a thin cylindrical shell, the longitudinal stress is assumed to be uniformly distributed through the wall thickness and acts parallel to the cylinder axis. The resisting force can be calculated by considering the cross-sectional area of the wall around the circumference of the cut:
Where:
- F_resist is the total resisting force provided by the shell wall
- σ_L is the longitudinal stress in the shell wall
- r is the internal radius of the cylindrical shell
- t is the wall thickness
Note that we use the internal radius r in this analysis, which is acceptable for thin shells where the difference between internal and external radii is small. The approximation becomes more accurate as the r/t ratio increases.
Derivation of the Formula
To derive the formula for longitudinal stress in a thin cylindrical shell, we apply the principle of equilibrium by equating the bursting force and the resisting force.
Equilibrium Condition
For the cylinder section to be in equilibrium, the bursting force must equal the resisting force:
Substituting the expressions we derived:
Solving for Longitudinal Stress
Solving for the longitudinal stress σ_L:
Simplifying by canceling common terms:
This is the fundamental formula for longitudinal stress in a thin-walled cylindrical shell subjected to internal pressure.
Final Longitudinal Stress Formula
The longitudinal stress in a thin-walled cylindrical shell is given by:
Where:
- σ_L is the longitudinal stress in the shell wall (tensile for internal pressure)
- p is the internal pressure
- r is the internal radius of the cylindrical shell
- t is the wall thickness
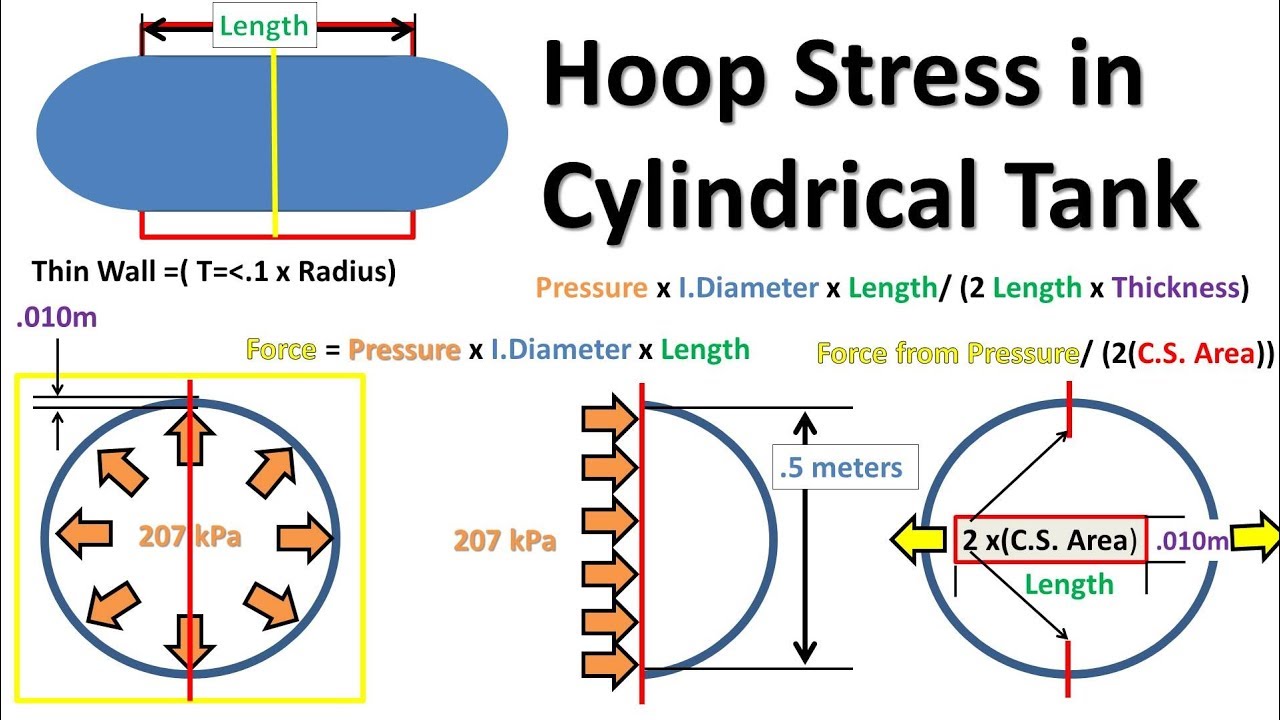
Comparison with Hoop Stress
Understanding the relationship between longitudinal stress and hoop stress is crucial for pressure vessel design and analysis.
Hoop Stress Formula
For comparison, the hoop stress in a thin cylindrical shell is given by:
Where σ_H is the hoop stress.
Relationship Between Stresses
Comparing the two formulas:
- Longitudinal Stress: σ_L = pr/(2t)
- Hoop Stress: σ_H = pr/t
This shows that:
The longitudinal stress is exactly half the hoop stress in a thin-walled cylindrical shell under internal pressure.
Physical Explanation
This relationship can be understood physically:
- Hoop Stress: Resists the circumferential force trying to split the cylinder along its length
- Longitudinal Stress: Resists the axial force trying to separate the end caps from the cylinder
- Force Distribution: The circumferential force acts around the entire circumference, while the axial force acts on the end area only
Design Implications
This relationship has important implications for pressure vessel design:
- Failure Mode: Cylindrical vessels typically fail by longitudinal splitting due to higher hoop stress
- Material Utilization: The cylinder material is not uniformly stressed, with hoop stress being critical
- Joint Design: Longitudinal joints must be designed for lower stress than circumferential joints
Sample Problems and Calculations
Let’s work through some sample problems to illustrate the application of the longitudinal stress formula for thin cylindrical shells.
Problem 1: Basic Stress Calculation
A cylindrical pressure vessel has an internal diameter of 1.2 meters and a wall thickness of 12 mm. If the vessel contains fluid at a pressure of 1.8 MPa, calculate both the longitudinal and hoop stresses in the vessel wall.
Given:
- Internal diameter D = 1.2 m, so internal radius r = 0.6 m
- Wall thickness t = 12 mm = 0.012 m
- Internal pressure p = 1.8 MPa = 1.8 × 10⁶ Pa
Solution:
First, check if the thin shell criterion is satisfied:
The thin shell assumption is valid.
Calculating longitudinal stress:
Calculating hoop stress:
Therefore:
- Longitudinal stress σ_L = 45 MPa
- Hoop stress σ_H = 90 MPa
- Verification: σ_L = σ_H/2 = 90/2 = 45 MPa ✓
Problem 2: Thickness Design Based on Longitudinal Stress
A cylindrical tank with an internal radius of 0.8 m is to contain a liquid at a maximum pressure of 1.2 MPa. If the allowable longitudinal stress in the tank material is 60 MPa, determine the minimum required wall thickness.
Given:
- Internal radius r = 0.8 m
- Internal pressure p = 1.2 MPa = 1.2 × 10⁶ Pa
- Allowable longitudinal stress σ_L_allow = 60 MPa = 60 × 10⁶ Pa
Solution:
Rearranging the longitudinal stress formula to solve for thickness:
Substituting values:
Therefore, the minimum required wall thickness is 8 mm.
Note: This calculation is based solely on longitudinal stress. In practice, hoop stress would also need to be checked, which would likely require a thicker wall since hoop stress is twice the longitudinal stress.
Problem 3: Pressure Rating Verification
A cylindrical pressure vessel has an internal diameter of 2 m and a wall thickness of 20 mm. If the material has an allowable longitudinal stress of 80 MPa, what is the maximum internal pressure the vessel can safely contain based on longitudinal stress considerations?
Given:
- Internal diameter D = 2 m, so internal radius r = 1 m
- Wall thickness t = 20 mm = 0.02 m
- Allowable longitudinal stress σ_L_allow = 80 MPa = 80 × 10⁶ Pa
Solution:
Rearranging the longitudinal stress formula to solve for pressure:
Substituting values:
Therefore, based on longitudinal stress considerations, the maximum safe internal pressure is 3.2 MPa.
Again, note that hoop stress would govern the actual pressure rating, which would be 1.6 MPa (half of 3.2 MPa) based on the same allowable stress.
Applications and Design Considerations
Understanding longitudinal stress is crucial for numerous engineering applications involving cylindrical pressure vessels.
Common Applications
Thin-walled cylindrical shells are used in many engineering applications:
- Pressure Vessels: Storage tanks, reactors, and process vessels
- Pipelines: Oil and gas transmission lines
- Aerospace: Rocket motor cases, fuel tanks, and fuselage sections
- Marine: Submarine hulls and underwater pipelines
- Automotive: Hydraulic cylinders and pneumatic systems
- Nuclear: Reactor pressure vessels and coolant systems
Design Factors
Several factors must be considered in the design of cylindrical pressure vessels:
- Safety Factors: Design stresses are typically limited to a fraction of the material’s yield strength
- Corrosion Allowance: Additional thickness to account for material loss over time
- Fabrication Tolerances: Variations in dimensions and quality during manufacturing
- Thermal Effects: Stresses due to temperature changes and thermal expansion
- Dynamic Loading: Effects of pressure fluctuations, vibration, and impact loads
Joint Design
Since cylindrical vessels are typically fabricated in sections, joint design is critical:
- Longitudinal Joints: Connect sections along the cylinder length, experience lower stress
- Circumferential Joints: Connect end caps to cylinder, experience higher stress
- Joint Efficiency: Welded joints typically have efficiency factors less than 1.0
- Inspection Requirements: Non-destructive testing to ensure joint quality
Advanced Considerations
For more complex applications or precise analysis, additional factors may need to be considered.
Thick Shell Analysis
When the r/t ratio approaches or falls below 10, thick shell analysis is required:
- Lame’s Equations: Provide exact solutions for thick cylindrical shells
- Stress Variation: Stresses vary through the wall thickness
- Maximum Stress Location: Maximum stresses occur at different locations for radial, hoop, and axial stresses
Thermal Stresses
Temperature variations can induce additional stresses:
- Thermal Expansion: Differential expansion between shell and contents
- Temperature Gradients: Non-uniform temperature distribution through wall thickness
- Combined Loading: Superposition of pressure and thermal stresses
External Pressure Effects
External pressure can significantly affect stress distribution:
- Compressive Stresses: External pressure creates compressive stresses
- Buckling Considerations: Compressive stresses can lead to structural instability
- Combined Internal and External Pressure: Requires careful analysis of net pressure effects
Standards and Codes
The design of pressure vessels is governed by various codes and standards:
- ASME Boiler and Pressure Vessel Code: Primary code in North America
- EN 13445: European standard for unfired pressure vessels
- JIS B 8265: Japanese industrial standard for pressure vessels
- GB 150: Chinese standard for steel pressure vessels
These codes provide detailed requirements for design, materials, fabrication, inspection, and testing of pressure vessels, including specific provisions for longitudinal stress analysis.
Comparison with Other Stress Types
Understanding how longitudinal stress compares with other stress types is important for comprehensive structural analysis.
| Stress Type | Direction | Formula | Magnitude (relative) | Typical Governing Factor |
|---|---|---|---|---|
| Longitudinal | Parallel to axis | σ_L = pr/(2t) | 1.0 | End cap design, axial loading |
| Hoop | Tangential to circumference | σ_H = pr/t | 2.0 | Vessel failure (splitting) |
| Radial | Radial direction | σ_r = -p (inner), 0 (outer) | ≈0 (thin shells) | Thick shell analysis |
Conclusion
The analysis of longitudinal stress in thin-walled cylindrical shells is a fundamental aspect of pressure vessel engineering that provides essential insights into the structural behavior of cylindrical pressure-containing components. The simple yet powerful formula σ_L = pr/(2t) enables engineers to quickly assess the longitudinal stress in cylindrical vessels under internal pressure.
The relationship between longitudinal stress and hoop stress (σ_L = σ_H/2) is particularly important for understanding why cylindrical vessels typically fail by longitudinal splitting rather than axial separation. This fundamental principle guides not only stress analysis but also design decisions regarding material selection, joint design, and safety factors.
The sample problems demonstrate practical applications of the longitudinal stress formula in three common engineering scenarios: calculating stresses for known geometry and pressure, determining required thickness for given loads, and establishing pressure ratings for existing vessels. These calculations form the foundation of pressure vessel design, though real-world applications require consideration of additional factors.
While the longitudinal stress is typically half the magnitude of hoop stress, it remains critically important in pressure vessel design. Longitudinal stress governs the design of end caps, flange connections, and supports, and must be considered in any comprehensive structural analysis.
Real-world design involves many considerations beyond basic stress calculations. Safety factors, material selection, joint design, corrosion allowances, and compliance with relevant codes and standards are all critical aspects of practical pressure vessel design. The thin shell assumption itself has limitations that must be recognized and addressed when appropriate.
For applications where the thin shell criterion is not satisfied, more complex thick shell analysis using Lame’s equations becomes necessary. Similarly, thermal stresses, dynamic effects, external pressure, and other loading conditions may require more sophisticated analysis techniques.
Modern computational methods, including finite element analysis, have enhanced our ability to analyze complex geometries and loading conditions that go beyond the simple analytical solutions. However, the fundamental principles embodied in the thin cylindrical shell stress formulas remain as important as ever for understanding and predicting structural behavior.
As engineering applications continue to demand higher pressures, more extreme temperatures, and greater reliability, the principles of stress analysis in cylindrical shells will continue to evolve. New materials, advanced manufacturing techniques, and improved analytical methods will enhance our ability to design even more efficient and reliable pressure vessels.
For students and practitioners of mechanical engineering, mastering the analysis of longitudinal stress in thin cylinders provides a solid foundation for understanding more complex structural problems. The concepts of equilibrium, stress distribution, and material behavior illustrated by this simple geometry are applicable to a wide range of engineering structures and systems.
In conclusion, the stress analysis of thin-walled cylindrical shells represents a perfect example of how fundamental engineering principles can be applied to solve practical design problems. The combination of theoretical analysis, practical considerations, and real-world applications makes this topic both intellectually satisfying and professionally valuable. Understanding longitudinal stress is essential for any engineer working with pressure vessels, pipelines, or other cylindrical structures subjected to internal or external pressure.