In the realm of thermodynamics and gas behavior, several fundamental laws govern how gases respond to changes in pressure, volume, and temperature. Among these, Avogadro’s Law holds a special place as one of the cornerstones of our understanding of ideal gas behavior. Named after the Italian scientist Amedeo Avogadro, this law provides crucial insights into the relationship between the volume of a gas and the amount of substance it contains, forming an essential link in the development of the Ideal Gas Law.
Avogadro’s Law, alongside Boyle’s Law and Charles’s Law, represents one of the fundamental gas laws that led to our modern understanding of gas behavior. While Boyle’s Law describes the inverse relationship between pressure and volume at constant temperature, and Charles’s Law describes the direct relationship between volume and temperature at constant pressure, Avogadro’s Law addresses how volume changes with the amount of gas when temperature and pressure are held constant.
Introduction to Avogadro’s Law
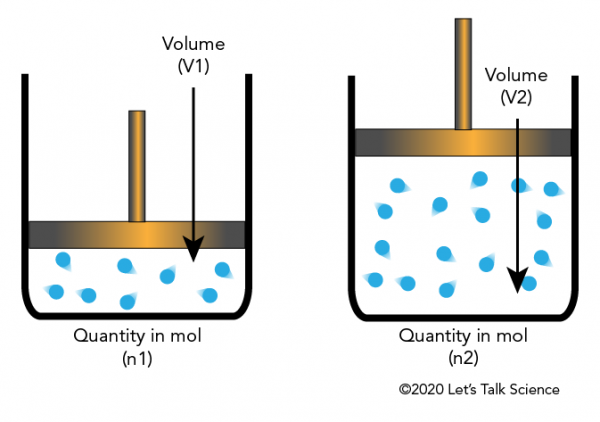
Avogadro’s Law is a gas law that states a fundamental relationship between the volume of a gas and the amount of substance (number of moles) it contains. This law was first formulated by Amedeo Avogadro in 1811 and provided a crucial insight that helped bridge the gap between macroscopic gas behavior and the microscopic nature of matter.
The law can be stated as follows:
This simple yet profound statement has far-reaching implications for our understanding of gas behavior and forms the foundation for many important concepts in chemistry and physics.
Statement of the Law
The mathematical representation of Avogadro’s Law expresses the direct proportionality between the volume of a gas and the number of moles of that gas when temperature and pressure are held constant:
This proportionality can be written as an equation by introducing a constant:
Where:
- V is the volume of the gas
- n is the number of moles of the gas
- k is a proportionality constant that depends on temperature and pressure
For comparing two different states of the same gas or two different gases under the same conditions, the law can be expressed as:
This form is particularly useful for solving problems involving changes in the amount of gas while maintaining constant temperature and pressure.
Mathematical Representation
The mathematical representation of Avogadro’s Law provides a quantitative framework for understanding and predicting gas behavior. Let’s explore this representation in more detail.
Proportionality Form
The fundamental relationship expressed by Avogadro’s Law is:
This means that if we double the number of moles of gas while keeping temperature and pressure constant, the volume will also double. Similarly, if we halve the number of moles, the volume will be halved.
Equation Form
Converting the proportionality to an equation:
The constant k depends on the specific conditions of temperature and pressure. At standard temperature and pressure (STP: 0°C and 1 atm), the value of k is approximately 22.4 L/mol for ideal gases.
Comparative Form
When comparing two different conditions with the same temperature and pressure:
This can also be written as:
This form is particularly useful for problem-solving applications where we need to calculate unknown volumes or amounts of gas.
Significance of Avogadro’s Law
Avogadro’s Law has profound significance in both theoretical and practical aspects of chemistry and physics. Its implications extend far beyond the simple mathematical relationship it describes.
Concept of the Mole
Avogadro’s Law is intimately connected to the concept of the mole, which is one of the fundamental units in the International System of Units (SI). The mole provides a bridge between the macroscopic world we can measure and the microscopic world of atoms and molecules.
Avogadro’s number (N_A) is defined as the number of particles (atoms, molecules, ions, etc.) in one mole of a substance:
This enormous number reflects the incredibly small size of individual atoms and molecules. The concept of the mole allows scientists to work with manageable quantities while still dealing with the vast numbers of particles involved in chemical reactions.
Universal Gas Constant
Avogadro’s Law played a crucial role in the development of the Universal Gas Constant (R_u), which appears in the Ideal Gas Law. The Universal Gas Constant relates the macroscopic properties of gases to the amount of substance:
The Universal Gas Constant is the same for all ideal gases, reflecting the universality expressed in Avogadro’s Law that equal volumes of different gases contain the same number of molecules under the same conditions.
Ideal Gas Law
Combining Avogadro’s Law with Boyle’s Law and Charles’s Law leads to the Ideal Gas Law, one of the most important equations in chemistry and physics:
Where:
- P is the absolute pressure of the gas
- V is the volume of the gas
- n is the number of moles of the gas
- R_u is the Universal Gas Constant
- T is the absolute temperature of the gas
The Ideal Gas Law incorporates all the fundamental gas laws into a single, comprehensive equation that describes the behavior of ideal gases under all conditions.
Practical Applications
Avogadro’s Law has numerous practical applications in engineering, chemistry, and physics. Understanding this law allows scientists and engineers to predict and control gas behavior in various systems.
Gas Volume Calculations
One of the most direct applications of Avogadro’s Law is in calculating gas volumes when the amount of substance changes:
This relationship is used in:
- Determining the volume of gas produced in chemical reactions
- Calculating the volume of gas needed for specific processes
- Scaling up or down gas handling systems
Stoichiometry Problems
In chemical reactions involving gases, Avogadro’s Law is essential for solving stoichiometry problems:
- Relating volumes of reactants and products in gas-phase reactions
- Determining limiting reactants in gas reactions
- Calculating yields of gaseous products
Industrial Gas Processing
Many industrial processes rely on the principles embodied in Avogadro’s Law:
- Ammonia synthesis (Haber process) where nitrogen and hydrogen gases react to form ammonia
- Petroleum refining processes involving gas separations
- Chemical vapor deposition processes in semiconductor manufacturing
Sample Problems and Solutions
Let’s explore some practical examples that demonstrate the application of Avogadro’s Law in solving real-world problems.
Problem 1: Volume Change with Amount Change
A balloon contains 2.5 moles of helium gas and has a volume of 50 liters at constant temperature and pressure. If 1.5 more moles of helium are added to the balloon, what will be the new volume?
Given:
- V₁ = 50 L
- n₁ = 2.5 mol
- n₂ = 2.5 mol + 1.5 mol = 4.0 mol
- V₂ = ?
Using Avogadro’s Law:
Substituting values:
Solving for V₂:
The new volume of the balloon will be 80 liters.
Problem 2: Determining Amount from Volume Change
A container holds 3.0 moles of nitrogen gas at a volume of 67.2 liters. If the volume is reduced to 44.8 liters while maintaining constant temperature and pressure, how many moles of nitrogen were removed?
Given:
- V₁ = 67.2 L
- n₁ = 3.0 mol
- V₂ = 44.8 L
- n₂ = ?
Using Avogadro’s Law:
Substituting values:
Solving for n₂:
The amount of nitrogen removed:
1.0 mole of nitrogen was removed from the container.
Problem 3: Application to Chemical Reactions
In the reaction: 2H₂(g) + O₂(g) → 2H₂O(g), if 50 liters of hydrogen gas react completely with oxygen at constant temperature and pressure, what volume of water vapor will be produced?
From the balanced equation, we see that 2 moles of H₂ produce 2 moles of H₂O, which means the volume ratio is 1:1 for this specific reaction.
Therefore, if 50 liters of H₂ react, 50 liters of H₂O will be produced.
Note: This simple relationship only works when the stoichiometric coefficients of the reactant and product gases are equal. In cases where they differ, we must use the mole ratios from the balanced equation.
Limitations and Real Gas Behavior
While Avogadro’s Law provides an excellent approximation for many gases under moderate conditions, it’s important to understand its limitations and when real gas behavior deviates from ideal behavior.
Assumptions of Ideal Gas Behavior
Avogadro’s Law, like all the fundamental gas laws, is based on the assumptions of ideal gas behavior:
- Point Particles: Gas molecules have negligible volume compared to the container
- No Intermolecular Forces: Gas molecules do not attract or repel each other
- Elastic Collisions: All collisions between gas molecules and with container walls are perfectly elastic
- Random Motion: Gas molecules move randomly in all directions
Deviation from Ideal Behavior
Real gases deviate from ideal behavior under certain conditions:
- High Pressure: At high pressures, the volume of gas molecules becomes significant compared to the container volume
- Low Temperature: At low temperatures, intermolecular forces become significant, causing attraction between molecules
- Polar Molecules: Gases with strong intermolecular forces (like water vapor) deviate more from ideal behavior
Van der Waals Equation
To account for real gas behavior, the Van der Waals equation modifies the Ideal Gas Law:
Where:
- a accounts for intermolecular attractive forces
- b accounts for the finite volume of gas molecules
Even with these corrections, Avogadro’s Law remains a useful approximation for many practical applications.
Historical Context and Development
Understanding the historical development of Avogadro’s Law provides insight into the scientific process and the evolution of our understanding of matter.
Amedeo Avogadro
Amedeo Avogadro (1776-1856) was an Italian scientist who proposed his law in 1811. Interestingly, his work was not widely accepted during his lifetime, partly because atomic theory was still controversial at the time.
Avogadro’s original hypothesis was:
This was a revolutionary idea that helped establish the molecular nature of matter.
Acceptance and Recognition
Avogadro’s Law gained acceptance primarily through the work of Stanislao Cannizzaro, who presented it at the Karlsruhe Congress in 1860. This conference was crucial in establishing atomic and molecular theory in chemistry.
The law was later confirmed through numerous experiments and became one of the cornerstones of modern chemistry and physics.
Connection to Other Gas Laws
Avogadro’s Law, together with Boyle’s Law and Charles’s Law, formed the foundation for the Ideal Gas Law:
- Boyle’s Law (1662): P ∝ 1/V (at constant n and T)
- Charles’s Law (1787): V ∝ T (at constant n and P)
- Avogadro’s Law (1811): V ∝ n (at constant P and T)
Combining these laws leads to the Ideal Gas Law:
Modern Applications and Extensions
Avogadro’s Law continues to find applications in modern science and technology, extending far beyond its original formulation.
Standard Temperature and Pressure (STP)
Avogadro’s Law is fundamental to defining standard conditions for gas measurements:
- Standard Temperature: 0°C (273.15 K)
- Standard Pressure: 1 atm (101.325 kPa)
- Molar Volume at STP: 22.414 L/mol
This standard molar volume is a direct consequence of Avogadro’s Law and is used extensively in chemical calculations.
Gas Density Calculations
Combining Avogadro’s Law with the definition of density allows for the calculation of gas densities:
Where M is the molar mass of the gas. Using Avogadro’s Law (V = kn):
This shows that at constant temperature and pressure, the density of a gas is directly proportional to its molar mass.
Partial Pressures and Dalton’s Law
Avogadro’s Law is also fundamental to understanding partial pressures in gas mixtures:
Each gas in a mixture contributes to the total pressure in proportion to its mole fraction, which is a direct application of Avogadro’s principle.
Experimental Verification
Avogadro’s Law can be experimentally verified through careful measurements of gas volumes and amounts under controlled conditions.
Experimental Setup
A typical experimental setup might include:
- A gas syringe or eudiometer for measuring volume changes
- A balance for measuring gas masses
- Temperature and pressure controls
- Gas collection and measurement apparatus
Procedure
The experimental procedure typically involves:
- Measuring the volume of a known amount of gas at specific temperature and pressure
- Changing the amount of gas while maintaining constant temperature and pressure
- Measuring the new volume
- Comparing the volume ratios to the amount ratios
Data Analysis
The data should show that V/n remains constant when temperature and pressure are held constant, confirming Avogadro’s Law.
Conclusion
Avogadro’s Law represents one of the fundamental principles that underpin our understanding of gas behavior and the molecular nature of matter. Its simple statement – that equal volumes of all ideal gases at the same temperature and pressure contain the same number of molecules – has profound implications for chemistry, physics, and engineering.
The law’s mathematical representation, V ∝ n (at constant P and T), provides a quantitative framework for predicting and calculating gas behavior in numerous practical applications. From determining reaction stoichiometry to designing industrial gas processing systems, Avogadro’s Law serves as an essential tool for scientists and engineers.
The significance of Avogadro’s Law extends beyond its immediate applications. It played a crucial role in the development of atomic theory and led directly to the concept of the mole and Avogadro’s number. These concepts form the bridge between the macroscopic world we can measure and the microscopic world of atoms and molecules.
Furthermore, Avogadro’s Law is one of the three fundamental gas laws that combine to form the Ideal Gas Law, one of the most important equations in science. This demonstrates how individual laws can be synthesized into more comprehensive theoretical frameworks.
While the law is based on the assumptions of ideal gas behavior and has limitations under extreme conditions, it remains remarkably accurate for many practical applications. Understanding when and how real gases deviate from ideal behavior allows scientists and engineers to apply corrections when necessary while still benefiting from the simplicity and utility of Avogadro’s Law.
The historical development of Avogadro’s Law illustrates the scientific process, showing how revolutionary ideas may initially face resistance before gaining acceptance through experimental verification and theoretical development. Today, the law is universally accepted and forms a cornerstone of modern chemistry and physics education.
In modern applications, Avogadro’s Law continues to be relevant in fields ranging from environmental science (understanding atmospheric gas behavior) to materials science (designing gas separation membranes) to biotechnology (optimizing fermentation processes). Its enduring relevance testifies to the fundamental nature of the principles it embodies.
As we continue to develop more sophisticated models of gas behavior and explore new states of matter, the insights provided by Avogadro’s Law remain valuable. Whether in the design of more efficient engines, the development of new materials, or the understanding of atmospheric processes, this fundamental law continues to provide the foundation for scientific and engineering advances.
Students and practitioners of science and engineering should not only memorize Avogadro’s Law but also understand its deeper implications for the nature of matter and energy. This understanding provides the conceptual framework necessary for tackling more complex problems in thermodynamics, chemical engineering, and related fields.